Continuous Variables
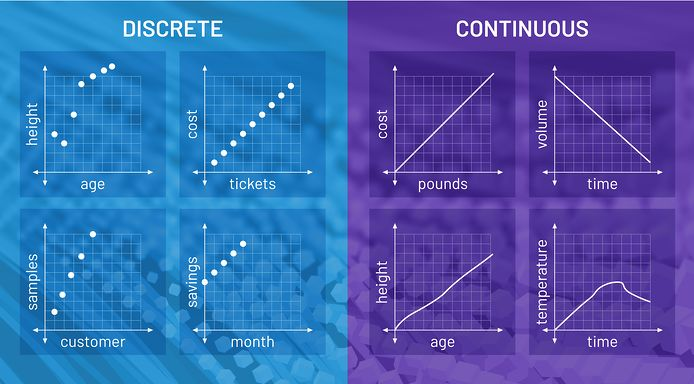
- A discrete variable is “countable” (has values that can be in a list)
- A continuous variable has values that cannot be written as a list (“uncountable”)
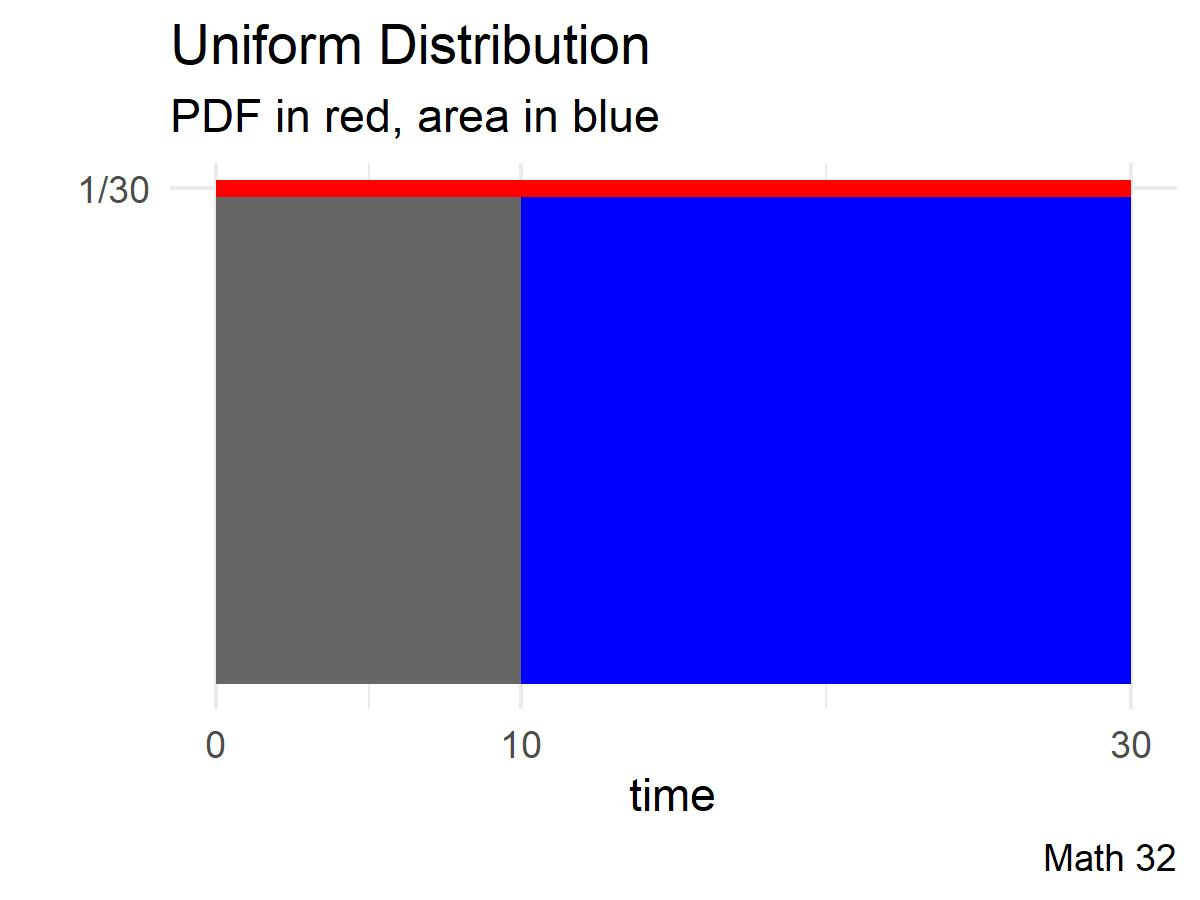
Uniform Distribution

You arrive at a bus stop at 10 o’clock, knowing that the bus will arrive at some time uniformly distributed between 10:00 and 10:30.
We build a probability density function (PDF) by ensuring that the area under the curve equals 100 percent (i.e. one square unit).

What is the probability that you will have to wait fewer than 12 minutes?

What is the probability that you will have to wait longer than 10 minutes?
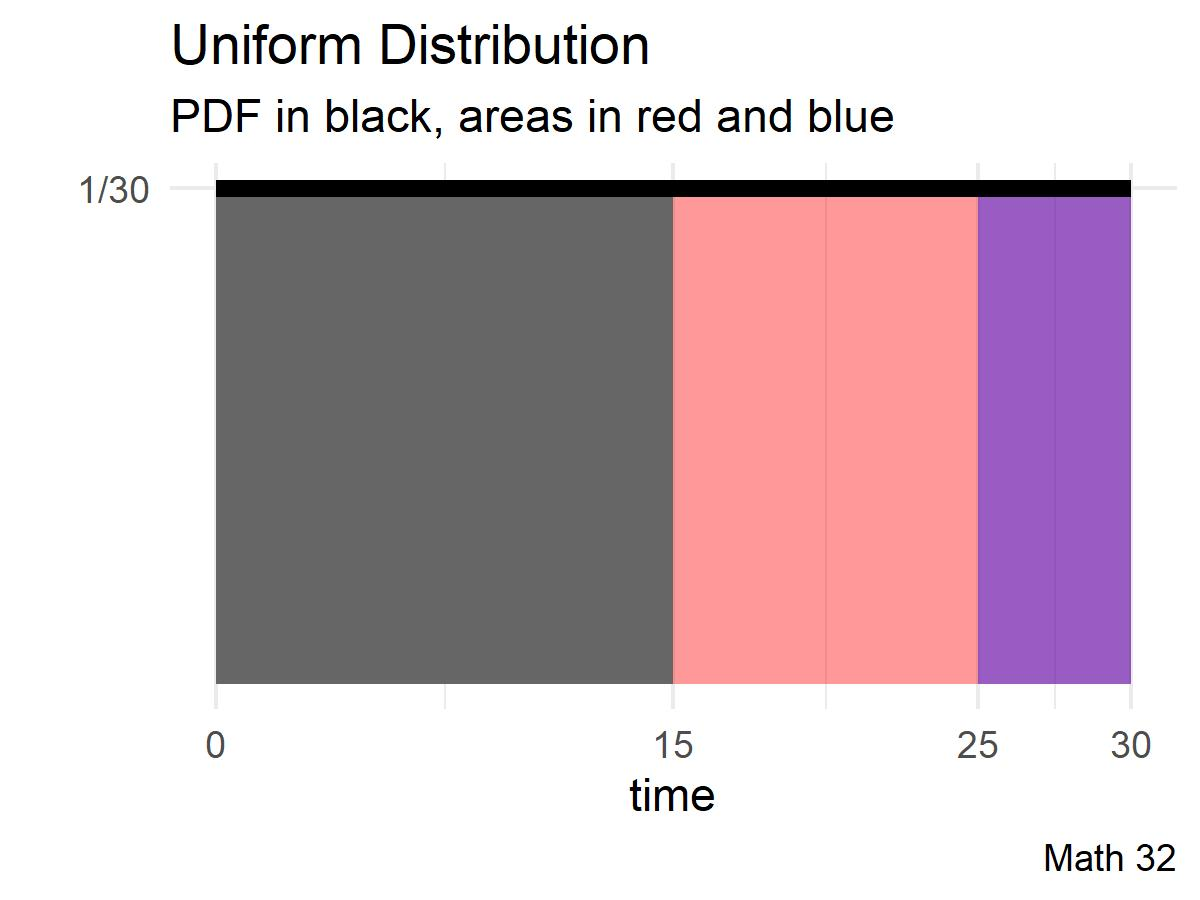
If at 10:15 the bus has not yet arrived, what is the probability that you will have to wait at least an additional 10 minutes?
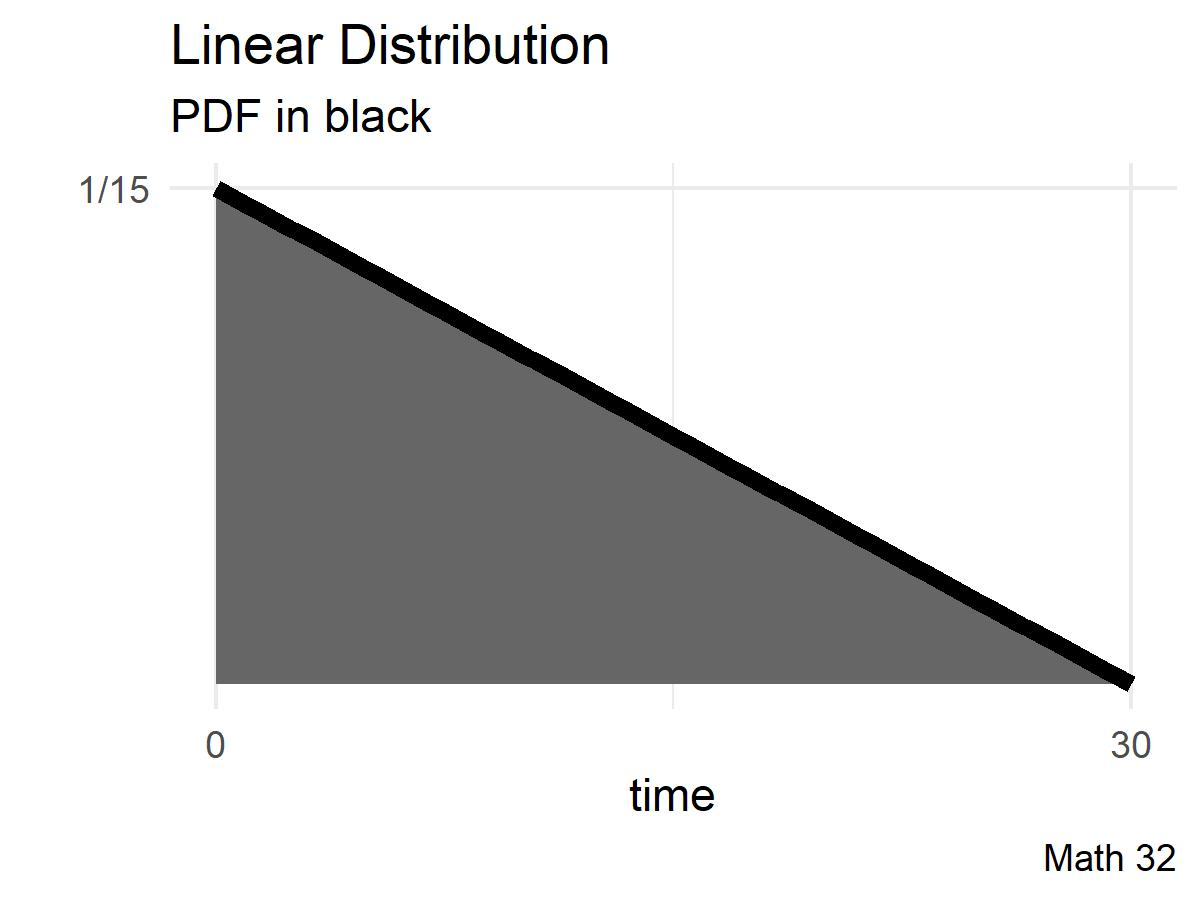
Linear Distribution

You arrive at a bus stop at 10 o’clock, knowing that the bus will arrive at some time linearly distributed between 10:00 and 10:30. The probability density function (PDF) is
\[f(x) = \begin{cases} -\displaystyle\frac{1}{450}x + \displaystyle\frac{1}{15} & 0 \leq x \leq 30 \\ 0 & \text{otherwise} \end{cases}\]
Probability Density Function (PDF)
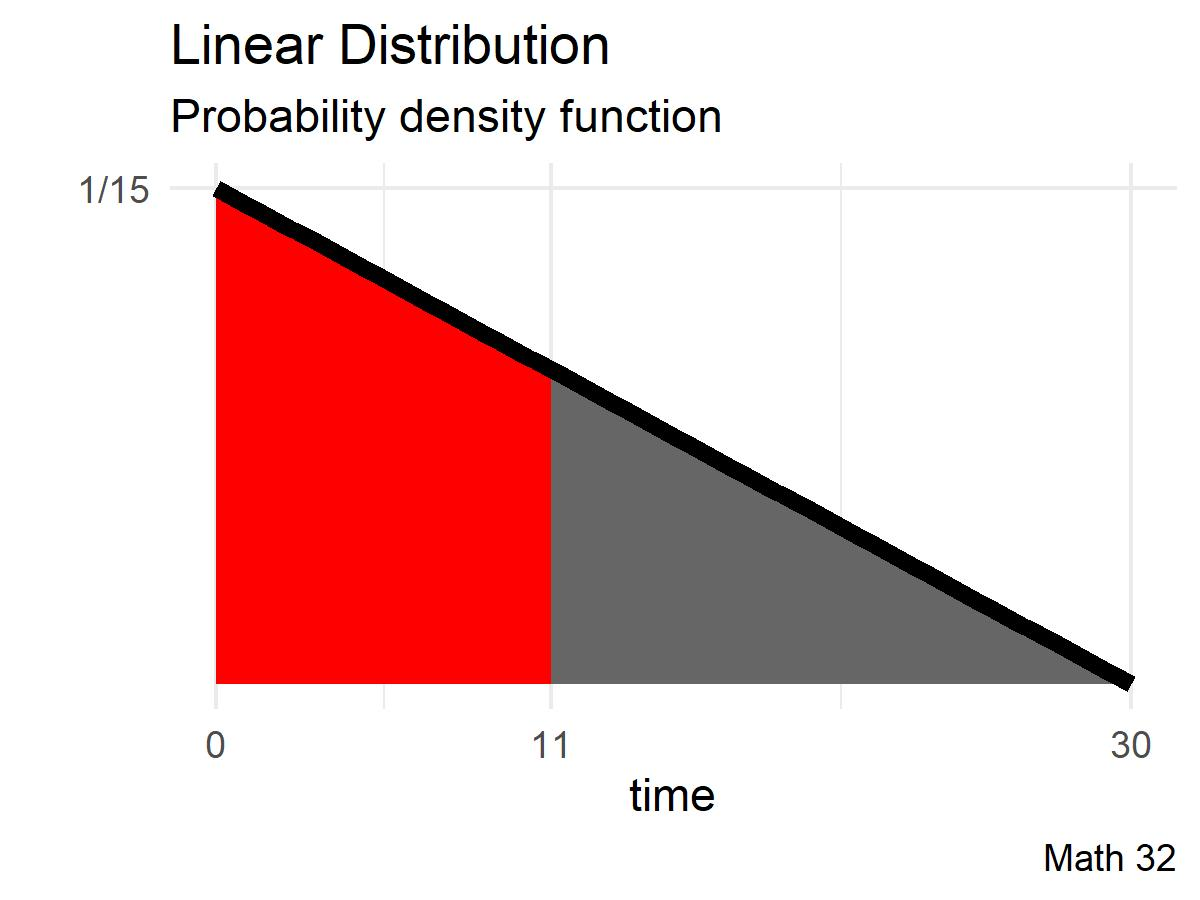
What is the probability that you will have to wait fewer than 7 minutes?
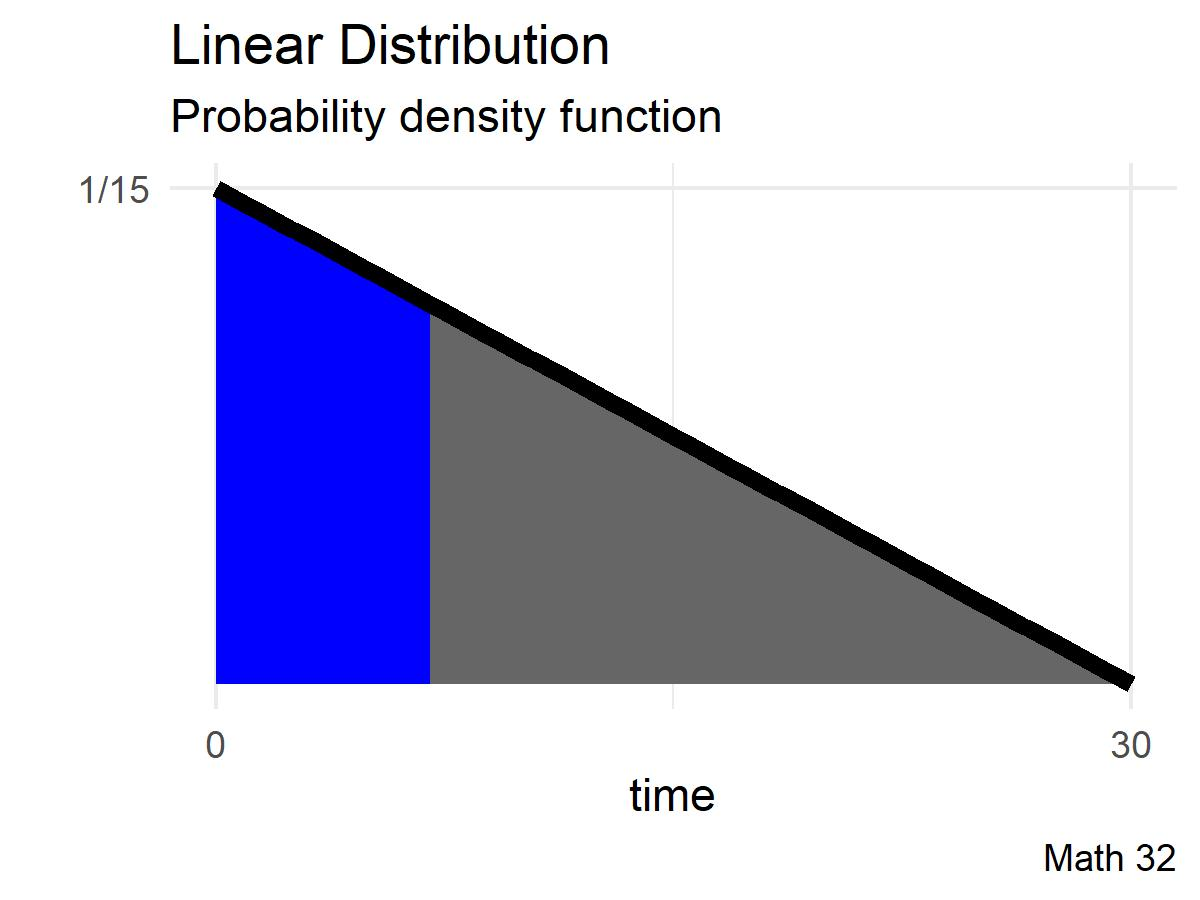
What is the probability that you will have to wait fewer than 11 minutes?
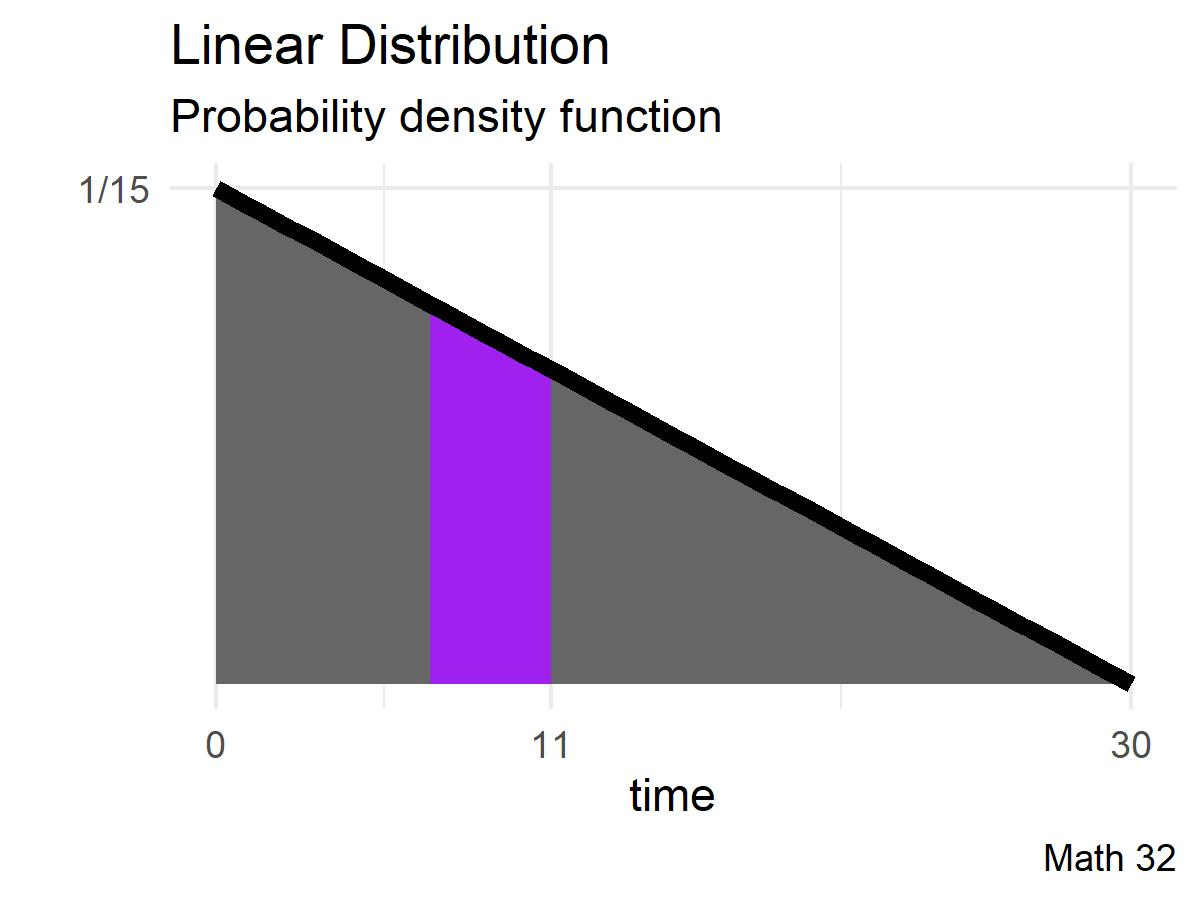
What is the probability that you will have to wait between 7 and 11 minutes?
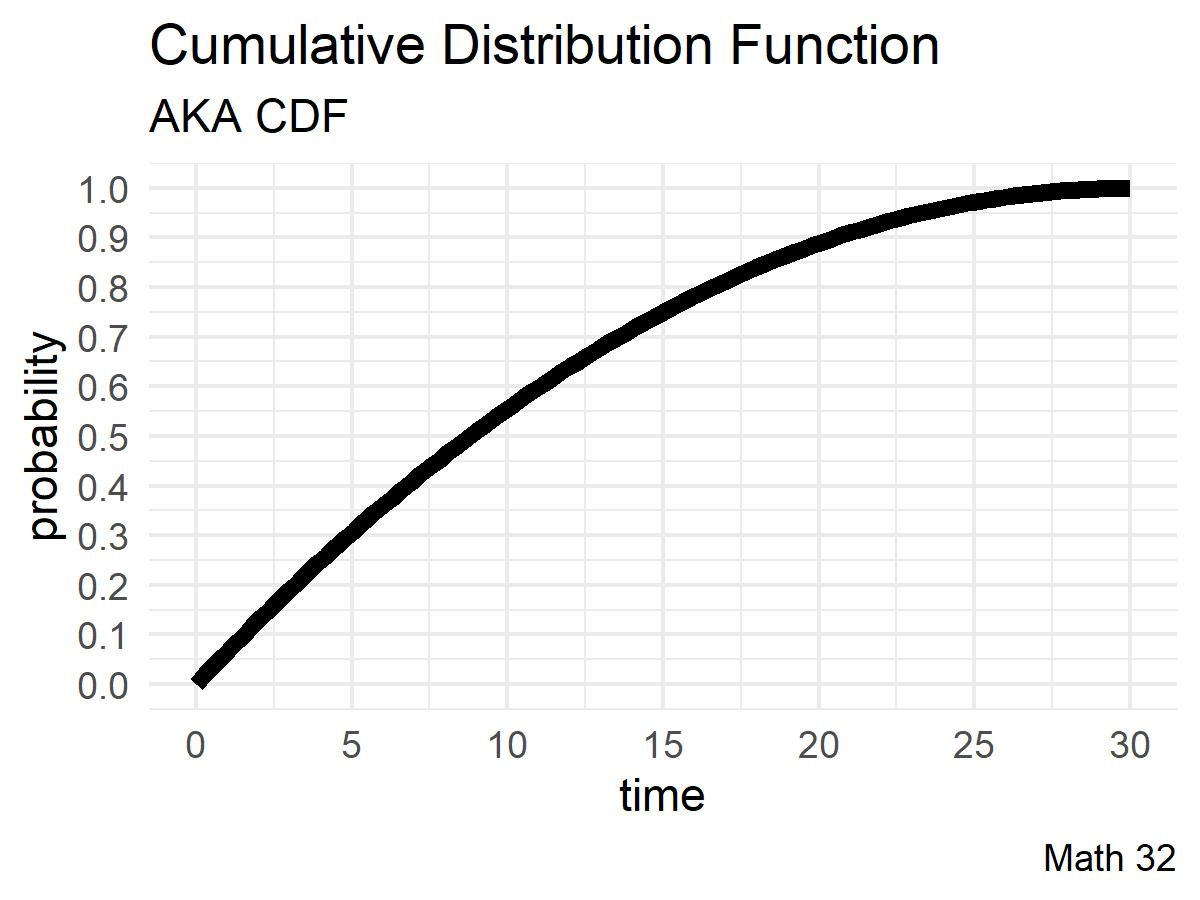
Cumulative Density Function
- There are no nonzero probabilities to the left. The CDF “starts with zero” probability. Here, \(F(0) = 0\)
- Since all probabilities add up to 100%, the CDF ends at one”. Here, \(F(30) = 1\)
Looking Ahead
- due Fri., Feb. 10:
- WHW5
- JHW3
- Demographics Survey Part 2
- Be mindful of before-lecture quizzes
No lecture session for Math 32:
- Feb 20, Mar 10, Mar 24
Exam 1 will be on Wed., Mar. 1
- more information in weekly announcements

